Data Representation & External Sorting Study Note
Data Representation
Relational database elements:
CREATE TABLE Product (
pid INT PRIMARY KEY, -- Base address (B)
name CHAR(20),
description VARHCAR(100),
maker CHAR(10) REFERENCES Company(name)
)
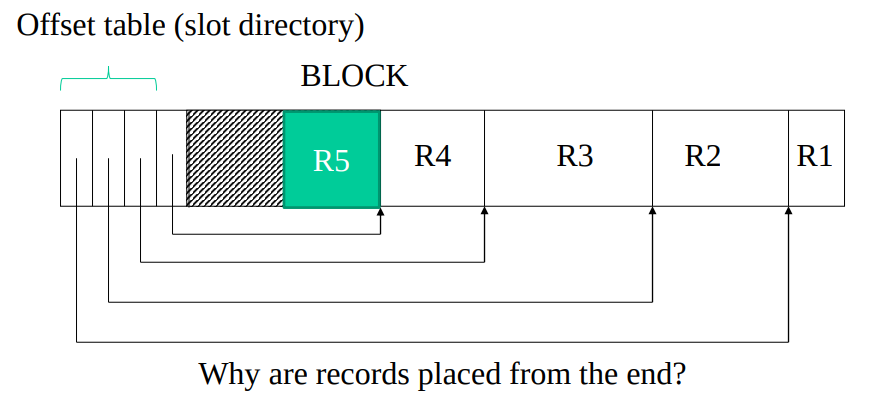
- A tuple/row is stored as a “record”
- The storing is similar to how computer stores blocks. We have a header for storing the metadata information, and blocks are stored sequentially after the header. The header includes pointers to blocks of records, length of records, and the timestamps that records the last modified or read time.
- However, differently, the header (offset table) and blocks are stored from both left and right because it’s easier to add a new block and its metadata information into the free space in the middle.
External Sorting
Problem: Sort large amount of data with little memory.
Basics
- A block on storage devices loaded into a page in main memory
- We sometimes interchange page with block
-
Buffer pages
- Often refer to pages in main memory used to store input, output, and intermediate data for an algorithm
- Run: a sorted sublist of input data
- Make a pass through data:
- Loading the entire data from disk once
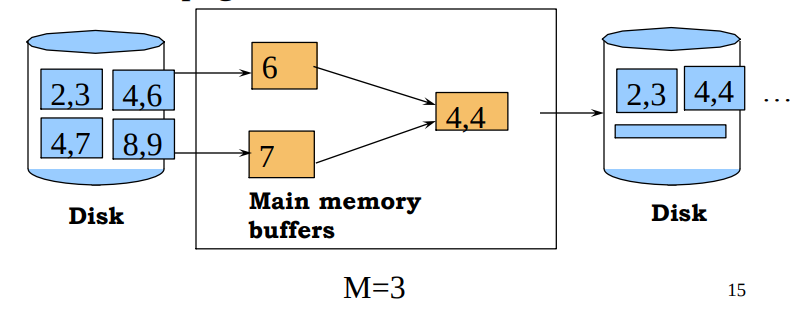
2-Way Merge-sort (Requires 3 Buffers)
- Pass 0: Read a page, sort it, write it
- only one input buffer page is used
- Pass 1, 2, …, etc.: merging two runs at a time
- two output buffer page is used
- in total, three buffer pages used.
- Each pass we read and write each page in file
- If there are $N$ pages in the file, it means that the number of passes are
$$\lceil \log_2{N} \rceil +1$$
- Total cost:
$$2N(\lceil \log_2{N} \rceil +1)$$
If we have more main memory…
- $M$: # of blocks (i.e., pages) in main memory
- $B(R)$: # of blocks of relation $R$
Example:
$M=5, B(R)=108$
- Sorting: load 5 pages, sort them, write back as run: $ \lceil 108/5 \rceil = \lceil 21.6 \rceil = 21 \text{ runs}$
- $21$ runs, $5$ pages/run ($21*5 = 105$ pages)
- $1$ run, $3$ pages/run
- Merging: $(M-1)$-way merging => 4-way merging
- take $4$ runs, $5$ pages/run ($20$-page run)
- how many runs?
External Merge-Sort
Pass 0 (Sorting)
- Load $M$ blocks in memory and sort
- Result: $\lceil \frac{B(R)}{M} \rceil$ sorted sublists of size $M$
- Each sorted sublist is a run
Pass 1/k (Merging)
- Merge $M – 1$ runs into a new run
- Result: each run has now $M (M – 1)$ blocks if this pass can finish.
- Result: usually, 1 pass of merging is not enough, so each run should have $M(M-1)^k$ blocks
Cost of External Merge Sort
- Number of passes: $1+\lceil \log_{M-1}{\lceil B(R)/M \rceil} \rceil$
- Cost: $2\cdot k\cdot B(R)$, where $k$ is number of passes including sorting.
Example
Consider external-sorting a table R which contains 120 blocks of data, using 4 pages of memory buffer.
That is, $B(R) = 120$ and $M = 4$. Note: use all available memory for sorting and merging.
- For each pass (sorting and merging), state the number of runs and the size of runs
generated by the pass.
- Pass 0 (use all pages to sort): Generate 30 runs, the size of each run is 4 pages.
- Pass 1 (3-way merge): Generate 10 runs, the size of each run is 12 blocks.
- Pass 2 (3-way merge): Generate 4 runs (3 runs having 36 blocks and 1 run having 12 blocks)
- Pass 3 (3-way merge): Generate 2 runs (1 run having 108 blocks and 1 run having 12 blocks)
- Pass 4 (2-way merge): Generate 1 sorted run of 120 blocks
- What is the total cost (measured by the number of block I/O’s) of this external-sorting? $\text{Total cost} = ( \text{# of passes} ) \times 2 \times ( \text{# of blocks} ) = 5 \times 2 \times 120 = 1200$
Or…
$\text{Total cost} = (1+\lceil \log_3{\lceil 120/4 \rceil} \rceil) \times 2 \times 120 =1200$